PROYECTILES COMPROBACIÒN CON CALCULADORA TI 92
 |
| Figura 4.11 El desplazamiento total s de un balón de fútbol en un punto de su recorrido. El vector tiene componentes y a lo largo de los ejes horizontal y vertical. Su magnitud es s y forma un ángulo Φ con la horizontal. |
Movimiento de proyectil
Objetivos de aprendizaje
Al final de esta sección, podrá:- Utilizar el movimiento unidimensional en direcciones perpendiculares para analizar el movimiento de proyectil.
- Calcular el alcance, el tiempo de vuelo y la altura máxima de un proyectil que se lanza e impacta en una superficie plana y horizontal.
- Encontrar el tiempo de vuelo y la velocidad de impacto de un proyectil que aterriza a una altura diferente a la del lanzamiento.
- Calcular la trayectoria de un proyectil.
El movimiento de proyectil es el movimiento de un objeto lanzado o proyectado al aire, sujeto únicamente a la aceleración como resultado de la gravedad. Las aplicaciones del movimiento de proyectil en física e ingeniería son numerosas. Algunos ejemplos son los meteoritos al entrar en la atmósfera terrestre, los fuegos artificiales y el movimiento de cualquier pelota en los deportes. Dichos objetos se denominan proyectiles y su recorrido se denomina trayectoria. El movimiento de los objetos que caen, tal y como se explica en Movimiento rectilíneo, es un tipo simple de movimiento de proyectil unidimensional en el que no hay movimiento horizontal. En esta sección, consideramos el movimiento bidimensional de proyectil, y nuestro tratamiento descarta los efectos de la resistencia del aire.
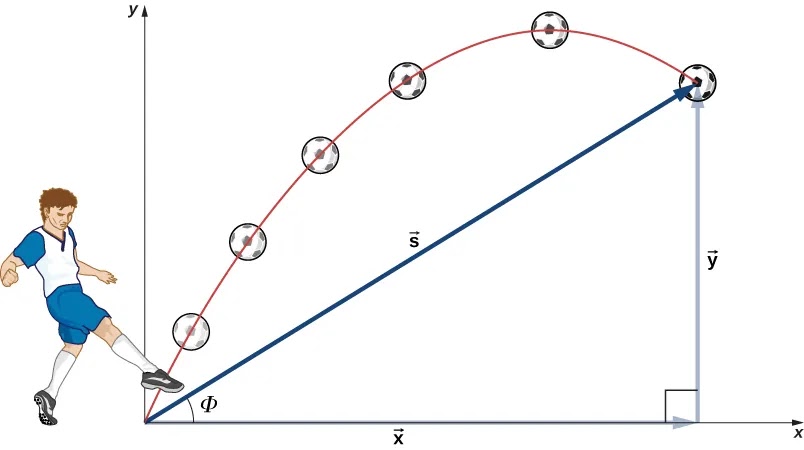
El hecho más importante que hay que recordar aquí es que los movimientos a lo largo de los ejes perpendiculares son independientes y, por tanto, pueden analizarse por separado. Ya hablamos de este hecho en Vectores de desplazamiento y velocidad, donde vimos que los movimientos verticales y horizontales son independientes. La clave para analizar el movimiento bidimensional de proyectil es dividirlo en dos movimientos: uno a lo largo del eje horizontal y otro a lo largo del vertical. (Esta elección de ejes es la más sensata porque la aceleración resultante de la gravedad es vertical; por lo tanto, no hay aceleración a lo largo del eje horizontal cuando la resistencia del aire es despreciable). Como es habitual, llamamos al eje horizontal eje de la x y al eje vertical eje de la y. No es necesario que utilicemos esta elección de ejes; simplemente es conveniente en el caso de la aceleración gravitatoria. En otros casos podemos elegir un conjunto diferente de ejes. La Figura 4.11 ilustra la notación para el desplazamiento, donde definimos Δe como el desplazamiento total, y ēx y ēy son sus vectores componentes a lo largo de los ejes horizontal y vertical, respectivamente. Las magnitudes de estos vectores son s, x y y.
OTRAS CÓNICAS
A continuación te presento una tabla con datos representativos de los planetas del Sistema Solar (excluyendo cuerpos menores) y, al final, un diagrama ASCII simplificado que ilustra de forma esquemática sus órbitas y el “movimiento” relativo alrededor del Sol. (Ten en cuenta que los valores son aproximados y la representación gráfica no está a escala; su finalidad es ilustrar el concepto de órbitas concéntricas y velocidades diferenciadas.)
Tabla con Datos de los Planetas
| Planeta | Distancia media al Sol (AU) | Masa (kg) | Excentricidad | Velocidad orbital (km/s) |
|---|---|---|---|---|
| Mercurio | 0.39 | 3.30×10²³ | 0.2056 | 47.87 |
| Venus | 0.723 | 4.87×10²⁴ | 0.00677 | 35.02 |
| Tierra | 1.0 | 5.97×10²⁴ | 0.0167 | 29.78 |
| Marte | 1.524 | 6.42×10²³ | 0.0934 | 24.08 |
| Júpiter | 5.203 | 1.90×10²⁷ | 0.0489 | 13.07 |
| Saturno | 9.537 | 5.68×10²⁶ | 0.0565 | 9.69 |
| Urano | 19.191 | 8.68×10²⁵ | 0.0460 | 6.81 |
| Neptuno | 30.07 | 1.02×10²⁶ | 0.0086 | 5.43 |
Notas aclaratorias:
Distancia (AU): La unidad astronómica (AU) equivale a la distancia media de la Tierra al Sol (aprox. 149.6 millones de km).
Excentricidad: Indica qué tan elíptica es la órbita (un valor de 0 sería una órbita perfectamente circular).
Velocidad orbital: Es la velocidad promedio a la que cada planeta se desplaza a lo largo de su órbita.
Representación Gráfica (ASCII) del Movimiento Orbital
La siguiente ilustración es un modelo muy esquemático en el que se muestran “anillos” concéntricos representando las órbitas de cada planeta. Recuerda que los planetas se desplazan a diferentes velocidades: los que están más próximos al Sol (como Mercurio y Venus) se mueven más rápido que los más alejados (como Neptuno).
(Diagrama simplificado del Sistema Solar)
.-------------------.
.' '.
: Neptuno :
: (30.07 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Urano :
: (19.191 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Saturno :
: (9.537 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Júpiter :
: (5.203 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Marte :
: (1.524 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Tierra :
: (1.0 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Venus :
: (0.723 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Mercurio :
: (0.39 AU) :
'._ _.'
'-----------'
||
[SOL]
Más Allá
Si te interesa profundizar en el movimiento planetario, podríamos analizar detalles como cómo la segunda ley de Kepler explica que los planetas se mueven más rápido al acercarse al Sol (perihelio) y más despacio al alejarse (afelio). También se podría ampliar con información sobre los satélites, cintas de asteroides y la influencia de la gravedad en las órbitas planetarias.
La gravedad es la fuerza central que determina la trayectoria y el movimiento de los planetas en el Sistema Solar. Veamos en detalle cómo influye:
Fuerza Centrífuga vs. Inercia: Cada planeta posee una velocidad tangencial que, según la primera ley de Newton, lo haría moverse en línea recta si no actuara ninguna otra fuerza. La gravedad del Sol actúa como una fuerza de atracción que lo desvía constantemente hacia el centro, transformando ese movimiento en una trayectoria curva (órbita). Esta interacción es lo que en física denominamos fuerza centrípeta.
La Ley de la Gravitación Universal: La atracción gravitatoria se describe con la fórmula:
donde:
es la fuerza gravitatoria.
es la constante de gravitación universal.
y son las masas del Sol y del planeta, respectivamente.
es la distancia entre sus centros. Esta fuerza decrece con el cuadrado de la distancia: cuanto mayor es la separación, menor es la fuerza que mantiene al planeta "atado" al Sol.
Órbitas Elípticas y las Leyes de Kepler: La gravedad no solo determina que los planetas orbiten, sino también la forma de sus trayectorias. La segunda ley de Kepler explica que el área barrida por el radio vector (la línea que une al planeta con el Sol) es constante en intervalos de tiempo iguales. Esto significa que:
En el perihelio (momento más cercano al Sol), la fuerza gravitatoria es mayor, el planeta acelera y su velocidad orbital es mayor.
En el afelio (momento más lejano del Sol), la atracción es menor, por lo que la velocidad disminuye.
Así, la gravedad y la inercia se equilibran creando órbitas elípticas.
Perturbaciones y Efectos Secundarios: Además del Sol, otros cuerpos (como otros planetas o lunas) ejercen una fuerza gravitatoria que puede generar pequeñas perturbaciones en las órbitas. Estas interacciones pueden modificar gradualmente parámetros orbitales tales como la excentricidad, la inclinación o incluso provocar resonancias orbitarias. Un ejemplo clásico es la precesión del perihelio de Mercurio, la cual se comprende mejor incorporando correcciones de la Relatividad General.
Representación Conceptual en ASCII:
A continuación te presento una tabla con datos representativos de los planetas del Sistema Solar (excluyendo cuerpos menores) y, al final, un diagrama ASCII simplificado que ilustra de forma esquemática sus órbitas y el “movimiento” relativo alrededor del Sol. (Ten en cuenta que los valores son aproximados y la representación gráfica no está a escala; su finalidad es ilustrar el concepto de órbitas concéntricas y velocidades diferenciadas.)
Tabla con Datos de los Planetas
| Planeta | Distancia media al Sol (AU) | Masa (kg) | Excentricidad | Velocidad orbital (km/s) |
|---|---|---|---|---|
| Mercurio | 0.39 | 3.30×10²³ | 0.2056 | 47.87 |
| Venus | 0.723 | 4.87×10²⁴ | 0.00677 | 35.02 |
| Tierra | 1.0 | 5.97×10²⁴ | 0.0167 | 29.78 |
| Marte | 1.524 | 6.42×10²³ | 0.0934 | 24.08 |
| Júpiter | 5.203 | 1.90×10²⁷ | 0.0489 | 13.07 |
| Saturno | 9.537 | 5.68×10²⁶ | 0.0565 | 9.69 |
| Urano | 19.191 | 8.68×10²⁵ | 0.0460 | 6.81 |
| Neptuno | 30.07 | 1.02×10²⁶ | 0.0086 | 5.43 |
Notas aclaratorias:
Distancia (AU): La unidad astronómica (AU) equivale a la distancia media de la Tierra al Sol (aprox. 149.6 millones de km).
Excentricidad: Indica qué tan elíptica es la órbita (un valor de 0 sería una órbita perfectamente circular).
Velocidad orbital: Es la velocidad promedio a la que cada planeta se desplaza a lo largo de su órbita.
Representación Gráfica (ASCII) del Movimiento Orbital
La siguiente ilustración es un modelo muy esquemático en el que se muestran “anillos” concéntricos representando las órbitas de cada planeta. Recuerda que los planetas se desplazan a diferentes velocidades: los que están más próximos al Sol (como Mercurio y Venus) se mueven más rápido que los más alejados (como Neptuno).
(Diagrama simplificado del Sistema Solar)
.-------------------.
.' '.
: Neptuno :
: (30.07 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Urano :
: (19.191 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Saturno :
: (9.537 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Júpiter :
: (5.203 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Marte :
: (1.524 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Tierra :
: (1.0 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Venus :
: (0.723 AU) :
'._ _.'
'-----------'
||
||
.-------------------.
.' '.
: Mercurio :
: (0.39 AU) :
'._ _.'
'-----------'
||
[SOL]
Explicación del diagrama:
Cada “caja” o bloque representa una órbita orbital en la que se desplaza el planeta, colocadas en orden decreciente de distancia al Sol.
La disposición es vertical para indicar la separación en el sistema, aunque en realidad las órbitas se trazan como anillos concéntricos alrededor del Sol.
La diferencia en las longitudes (mención de AU) sirve para visualizar la escala relativa, sin ser una representación geométrica exacta.
Más Allá
Si te interesa profundizar en el movimiento planetario, podríamos analizar detalles como cómo la segunda ley de Kepler explica que los planetas se mueven más rápido al acercarse al Sol (perihelio) y más despacio al alejarse (afelio). También se podría ampliar con información sobre los satélites, cintas de asteroides y la influencia de la gravedad en las órbitas planetarias. ¿Te gustaría explorar alguno de estos temas o profundizar en algún aspecto en particular?
La gravedad es la fuerza central que determina la trayectoria y el movimiento de los planetas en el Sistema Solar. Veamos en detalle cómo influye:
Fuerza Centrífuga vs. Inercia: Cada planeta posee una velocidad tangencial que, según la primera ley de Newton, lo haría moverse en línea recta si no actuara ninguna otra fuerza. La gravedad del Sol actúa como una fuerza de atracción que lo desvía constantemente hacia el centro, transformando ese movimiento en una trayectoria curva (órbita). Esta interacción es lo que en física denominamos fuerza centrípeta.
La Ley de la Gravitación Universal: La atracción gravitatoria se describe con la fórmula:
donde:
es la fuerza gravitatoria.
es la constante de gravitación universal.
y son las masas del Sol y del planeta, respectivamente.
es la distancia entre sus centros. Esta fuerza decrece con el cuadrado de la distancia: cuanto mayor es la separación, menor es la fuerza que mantiene al planeta "atado" al Sol.
Órbitas Elípticas y las Leyes de Kepler: La gravedad no solo determina que los planetas orbiten, sino también la forma de sus trayectorias. La segunda ley de Kepler explica que el área barrida por el radio vector (la línea que une al planeta con el Sol) es constante en intervalos de tiempo iguales. Esto significa que:
En el perihelio (momento más cercano al Sol), la fuerza gravitatoria es mayor, el planeta acelera y su velocidad orbital es mayor.
En el afelio (momento más lejano del Sol), la atracción es menor, por lo que la velocidad disminuye.
Así, la gravedad y la inercia se equilibran creando órbitas elípticas.
Perturbaciones y Efectos Secundarios: Además del Sol, otros cuerpos (como otros planetas o lunas) ejercen una fuerza gravitatoria que puede generar pequeñas perturbaciones en las órbitas. Estas interacciones pueden modificar gradualmente parámetros orbitales tales como la excentricidad, la inclinación o incluso provocar resonancias orbitarias. Un ejemplo clásico es la precesión del perihelio de Mercurio, la cual se comprende mejor incorporando correcciones de la Relatividad General.
Representación Conceptual en ASCII:
Gravedad (F = G * m_sol * m_planeta / r^2)
│
▼
[ Sol ]
│
──────────────► │ ◄─────────────
Inercia (velocidad tangencial)
│
▼
[ Planeta ]
│
(La atracción gravitatoria desvía el movimiento
rectilíneo del planeta, generando una órbita
elíptica alrededor del Sol)
En este diagrama, la fuerza de gravedad actúa como una "cuerda invisible" que tira constantemente del planeta hacia el Sol, mientras la inercia tiende a mover el planeta en línea recta. La combinación de ambos da lugar a la trayectoria orbital.
Más Allá:
Si te interesa profundizar, podríamos explorar cómo la Relatividad General ajusta la comprensión del campo gravitatorio en zonas de alta masa concentrada (como en el caso del avance del perihelio de Mercurio), o cómo las perturbaciones gravitatorias entre planetas pueden dar lugar a resonancias orbitales complejas.
La gravedad es la fuerza fundamental que rige el movimiento de los cometas en el Sistema Solar. Aunque los cometas se comportan de manera similar a los planetas en cuanto a que orbitan alrededor del Sol, sus trayectorias, generalmente muy elípticas y a veces casi parabólicas, hacen que la influencia gravitatoria tenga efectos únicos sobre ellos. A continuación, se explica cómo la gravedad afecta el movimiento de los cometas:
1. Movimiento Orbital y Variación de Velocidad
Órbitas Elípticas y Hiperbólicas: Los cometas suelen moverse en trayectorias con alta excentricidad. Esto significa que, en su perihelio (el punto más cercano al Sol), la atracción gravitatoria es mucho mayor, lo que acelera al cometa significativamente. En cambio, al alejarse hasta el afelio, la fuerza disminuye y el cometa se desplaza más lentamente. La ley de gravitación universal rige este comportamiento:
donde el incremento drástico de la fuerza (al disminuir ) en el perihelio causa una aceleración notable.
Conservación del Momento Angular: Aunque la velocidad varía a lo largo de la órbita, la conservación del momento angular obliga al cometa a “compensar” estos cambios: cuando se acerca al Sol, su velocidad aumenta, y cuando se aleja, disminuye. Esto le permite recorrer trayectorias elípticas (o en algunos casos, trayectorias parabólicas o hiperbólicas en cometas de paso único).
2. Efectos de la Sublimación
Liberación de Gas y Polvo: Al acercarse al Sol, el calor hace que los hielos del cometa se sublimen, liberando gas y partículas de polvo. Aunque este proceso es térmico, tiene un efecto indirecto en la dinámica del cometa: el "empuje" de la sublimación genera pequeñas fuerzas (a veces descritas como “propulsores naturales”) llamadas efectos de outgassing.
Modificación de la Trayectoria: Estas pequeñas fuerzas pueden alterar levemente la trayectoria del cometa, sumándose a las variaciones impuestas por la gravedad. En ocasiones, si el cometa tiene mucho material liberado de forma asimétrica, su órbita puede cambiar con el paso de los años.
3. Perturbaciones Gravitacionales por Cuerpos Mayores
Interacción con Planetas: Cometas que pasan cerca de planetas masivos, en particular Júpiter, pueden experimentar perturbaciones gravitacionales significativas. Estas interacciones pueden:
Modificar la excentricidad y la inclinación de la órbita.
Alterar la energía orbital del cometa, lo que en algunos casos lo puede “capturar” en una órbita más cerrada o, por el contrario, expulsarlo del Sistema Solar.
Este fenómeno se debe a la poderosa atracción gravitatoria de planetas gigantes, que, al interactuar con el cometa, modifican su trayectoria de manera similar a un “efecto honda gravitatoria”.
4. Representación Conceptual con Diagrama ASCII
El siguiente diagrama ASCII ilustra, de manera simplificada, cómo interactúa la gravedad en el movimiento de un cometa:
Explicación del diagrama:
El Sol se encuentra en uno de los focos de la órbita elíptica del cometa.
Al acercarse al perihelio, el cometa experimenta una mayor aceleración por la gravedad, lo que se refleja en su alta velocidad en ese segmento de la órbita.
Al alejarse hacia el afelio, la fuerza gravitatoria disminuye y, consecuentemente, la velocidad disminuye.
Las flechas indican los cambios en la velocidad y la dirección del movimiento influenciados por la gravedad.
Conclusiones y Más Allá
En resumen, la gravedad actúa de manera decisiva sobre los cometas:
Define su trayecto: La atracción del Sol determina que sigan órbitas elípticas, parabólicas o hiperbólicas.
Modula la velocidad: Las variaciones gravitatorias impulsan cambios en la velocidad que son cruciales para el comportamiento orbital.
Interactúa con otros cuerpos: Perturbaciones causadas por planetas grandes pueden alterar radicalmente la trayectoria de un cometa.
Además, la combinación de la gravedad y los efectos de outgassing hace que el movimiento de los cometas sea dinámico y, a veces, impredecible. Esto ha permitido a los astrónomos aprender más sobre la dinámica del Sistema Solar, ya que el estudio de las trayectorias cometarias ofrece pistas sobre interacciones gravitatorias complejas y la historia de nuestra vecindad cósmica.
Podemos profundizar en ambas perspectivas, ya que entender cómo se calculan estas perturbaciones nos ayuda a comprender, igualmente, ejemplos históricos en los que han tenido un papel determinante en la evolución de la órbita de un cometa. A continuación, te presento un resumen completo de ambos enfoques:
1. Cálculo de las Perturbaciones Gravitatorias
Cuando hablamos de órbitas en el Sistema Solar, entendemos que ningún cuerpo se mueve en completa soledad. La interacción gravitatoria entre múltiples objetos (por ejemplo, el Sol, un cometa y un planeta cercano) se conoce como el problema de N-cuerpos. Dado que la solución analítica exacta para sistemas de más de dos cuerpos es extremadamente compleja o incluso imposible en forma cerrada, los astrónomos emplean dos tipos principales de métodos:
a) Métodos Analíticos: La Teoría de Perturbaciones
Elementos Oscilatorios y Variación de Elementos Orbitales: Se empieza considerando la órbita "ideal" del cometa (por ejemplo, una elipse descrita por sus elementos orbitales: semieje mayor, excentricidad, inclinación, etc.). La fuerza perturbadora de un planeta (u otro cuerpo) se introduce como un término adicional al potencial gravitatorio principal del Sol. La variación en cada uno de los elementos se puede calcular a partir de las ecuaciones de variación de Gauss o las ecuaciones planetarias de Lagrange. Estas ecuaciones relacionan las componentes de la fuerza perturbadora en la dirección radial, transversal y normal con la tasa de cambio de cada elemento orbital.
Promedio por Órbita y Aproximaciones: Debido a que las perturbaciones suelen ser pequeñas en cada vuelta, se hace un promedio (o "promedio secular") sobre la órbita completa. Este proceso permite aislar los cambios a largo plazo de los elementos orbitales, descartando variaciones periódicas de corta duración.
b) Métodos Numéricos
Integración Directa de las Ecuaciones de Movimiento: Aquí se utilizan algoritmos numéricos (por ejemplo, Runge-Kutta o integradores simétricos como el leapfrog) para resolver las ecuaciones de movimiento de todo el sistema en pequeños incrementos de tiempo. Estos métodos permiten incorporar la influencia de todos los cuerpos relevantes y seguir, paso a paso, cómo la órbita de un cometa se ve modificada tras un encuentro cercano o incluso tras múltiples encuentros.
Simulaciones por Computadora: Con la potencia computacional actual, se pueden simular interacciones complejas durante miles o millones de años, lo que nos ayuda a prever la evolución orbital de los cometas e incluso a identificar posibles colisiones o expulsiones del Sistema Solar.
Diagrama ASCII: Proceso de Cálculo de Perturbaciones
En resumen, el método elegido (analítico o numérico) depende de la complejidad del sistema y de la precisión requerida.
2. Ejemplos Históricos de Perturbaciones en Cometas
Explorar ejemplos concretos ayuda a visualizar cómo las perturbaciones no son solo conceptos teóricos, sino fenómenos que se han comprobado a lo largo del tiempo:
a) Cometa Shoemaker-Levy 9
Contexto: En 1992, el cometa Shoemaker-Levy 9 fue capturado por la gravedad de Júpiter tras un encuentro cercano. La intensa atracción tidal de Júpiter terminó fragmentando el cometa.
Perturbación Significativa: La interacción gravitatoria no sólo alteró su trayectoria, sino que también modificó sus características estructurales. De hecho, sus fragmentos impactaron en Júpiter en 1994, ofreciendo la primera observación directa del impacto de un cuerpo celeste en otro planeta.
b) Halley y otros Cometas Cíclicos
Cometa Halley: La órbita del Cometa Halley ha sido estudiada durante siglos. Se sabe que las interacciones gravitatorias, en particular con Júpiter y Saturno, modifican gradualmente sus parámetros orbitales. Estos cambios explican en parte las variaciones en la periodicidad observada a lo largo de la historia.
Cometa 2P/Encke: Otro ejemplo es el Cometa Encke, cuya órbita muy compacta y su corta periodicidad se deben, en parte, a perturbaciones repetidas con planetas como Júpiter. Estas interacciones han llevado a una evolución constante de sus parámetros orbitales, haciendo que su predicción requiera cálculos muy precisos de perturbaciones.
c) Otros Casos Notables
Fragmentación y Captura: Algunos cometas que realizan "encuentros cercanos" con planetas pueden ser alterados de forma tan drástica que cambian de una órbita parabólica a una elíptica, o incluso ser expulsados del Sistema Solar. Estos eventos ofrecen información crítica sobre la dinámica y estabilidad a largo plazo de los cuerpos helados en nuestro entorno solar.
Conclusión y Perspectivas Futuras
Las perturbaciones gravitatorias no solo son fundamentales para explicar la evolución orbital de los cometas, sino que también permiten a los astrónomos comprender la distribución de materia en el Sistema Solar. Al aplicar métodos analíticos y numéricos se pueden predecir con cierta precisión futuras trayectorias, lo que resulta vital tanto para la planificación de misiones espaciales como para evaluar riesgos de impacto.
Es fascinante ver cómo un encuentro aparentemente lejano con un gigante gaseoso puede definir el destino de un cometa entero, alterando su camino de forma notable.
¿Cómo se aplican las ecuaciones de variación de Gauss?¿Cuáles son algunos otros cometas con trayectorias notables?¿Qué métodos numéricos se utilizan en estudios de cometas?
A continuación, te ofrezco un análisis detallado que abarca tres aspectos fundamentales para comprender la dinámica de los cometas en presencia de perturbaciones gravitatorias:
1. Aplicación de las Ecuaciones de Variación de Gauss
Las ecuaciones de variación de Gauss son herramientas esenciales en mecánica celeste que permiten calcular cómo varían los elementos orbitales (por ejemplo, el semieje mayor, la excentricidad, la inclinación, el nodo ascendente, el argumento del perihelio y la anomalía) de un cuerpo en órbita cuando se introduce una fuerza perturbadora, además de la atracción gravitatoria principal (la del Sol, por ejemplo).
¿Cómo se aplican?
Descomposición de la Fuerza Perturbadora: La fuerza perturbadora se descompone en tres componentes:
Radial (R): A lo largo del radio vector que une el cometa con el Sun.
Transversal (T): En la dirección tangencial al movimiento orbital.
Normal (N): Perpendicular al plano orbital.
Proyección en Ejes Orbitales: Cada una de estas componentes influye de forma diferenciada sobre los elementos orbitales. Por ejemplo, la tasa de cambio del semieje mayor “” se expresa de forma general como:
Donde:
es la frecuencia media (o movimiento angular) del cometa.
es la excentricidad.
es la anomalía verdadera (el ángulo que describe la posición actual del cometa en su órbita).
es la distancia instantánea al Sol.
De manera similar, existen ecuaciones para la evolución de la excentricidad, de la inclinación y de los demás elementos, donde cada derivada depende de las componentes R, T y N.
Integración y Promedio: Una vez obtenidas las tasas de cambio, se pueden integrar estas ecuaciones, ya sea:
Analíticamente: En casos simplificados o mediante promedios sobre un periodo orbital (se secularizan los términos para obtener cambios a largo plazo).
Numéricamente: Para considerar efectos complejos y cambios no lineales en la órbita.
Estas ecuaciones, derivadas mediante métodos como los de Lagrange, permiten no solo analizar perturbaciones puntuales (por ejemplo, la influencia de un encuentro cercano) sino también evaluar cómo se acumulan los efectos a lo largo del tiempo.
2. Ejemplos de Cometas con Trayectorias Notables
Si bien el Cometa Halley es quizá el ejemplo más icónico, existen otros cometas cuyas trayectorias han llamado la atención de los astrónomos:
Cometa Halley (1P/Halley): Su órbita periódica (aproximadamente 76 años) se ha visto modificada por encuentros con planetas como Júpiter y Saturno. Las variaciones en su excentricidad y orientación han sido fundamentales para entender las perturbaciones en órbitas de largo plazo.
Cometa Encke (2P/Encke): Con un periódico de unos 3.3 años, su órbita es especialmente interesante porque, a lo largo de miles de ciclos, presenta modificaciones notables impulsadas por interacciones gravitatorias, además de los efectos de sublimación. Esto lo posiciona como un ejemplo del delicado equilibrio entre perturbaciones gravitatorias y efectos no gravitatorios.
Cometa Swift-Tuttle (109P/Swift-Tuttle): Este cometa, de gran tamaño y con una órbita que genera las Perseidas, tiene una trayectoria compleja. Su evolución orbital ha sido objeto de estudio para evaluar la influencia de perturbaciones periódicas y la estabilidad a largo plazo, además de la importancia de encuentros cercanos con cuerpos masivos.
Cometa Lovejoy (C/2011 W3): Conocido como un cometa rasante, Lovejoy se acercó significativamente al Sol. Su trayectoria es notable debido a la interacción entre la intensa atracción gravitatoria solar y la física de disipación (por ejemplo, sublimación extrema y fragmentación) durante su paso por la corona solar.
Cometa ISON (C/2012 S1): Aunque tristemente se desintegró en su acercamiento al Sol, ISON fue objeto de un análisis exhaustivo por lo que pudo enseñarnos sobre cómo la gravedad y los efectos térmicos pueden modificar drásticamente la estructura y trayectoria de un cometa.
3. Métodos Numéricos en Estudios de Cometas
Debido a la complejidad del sistema y a la imposibilidad de obtener soluciones cerradas en configuraciones de múltiples cuerpos (el problema de N-cuerpos), se recurre a diversos métodos numéricos para simular la evolución orbital de los cometas:
Integración de Runge-Kutta: Los métodos RK (como el RK4 o versiones adaptativas tipo RK45) permiten integrar las ecuaciones de movimiento en intervalos pequeños, garantizando precisión en condiciones de alta variabilidad (por ejemplo, durante un encuentro cercano con un planeta).
Integradores Simétricos (Leapfrog): Estos métodos son especialmente valorados en simulaciones de larga duración ya que conservan las propiedades conservativas del problema (energía, momento angular). Así, se minimizan los errores acumulativos en la integración a lo largo del tiempo.
Métodos Adaptativos (Bulirsch-Stoer, etc.): Algoritmos que adaptan el tamaño del paso de integración en función de la dinámica local. Son útiles en situaciones donde el cometa experimenta cambios bruscos en aceleración, como en acercamientos extremos al Sol o planetas.
Integradores Específicos para N-Cuerpos (por ejemplo, el Wisdom-Holman): Diseñados para sistemas planetarios, estos métodos simulan la interacción de múltiples cuerpos de manera eficiente, permitiendo rastrear la evolución de la órbita del cometa cuando se somete a varias perturbaciones simultáneas.
Comentarios
Publicar un comentario